Inhaltsverzeichnis
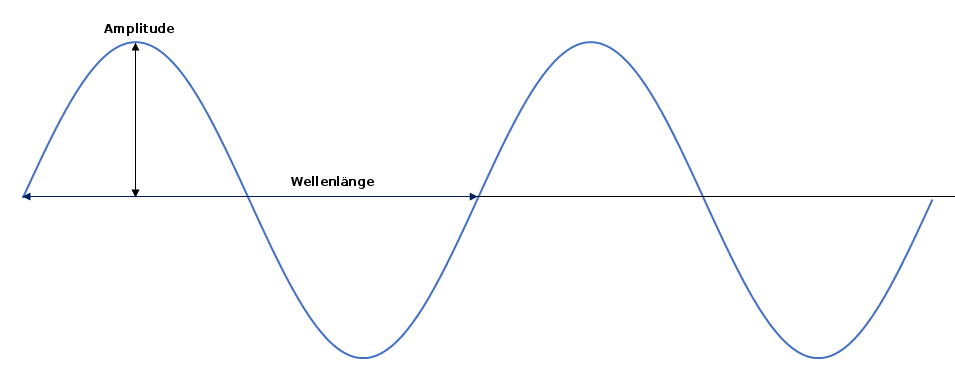
Wellenlänge
Die Wellenlänge (\lambda) beschreibt den kleinsten Abstand zweier Punkte gleicher Phase.
Die Amplitude ist der Maximalwert der Schwingung während einer Periode.
Formel
\lambda = (\frac{c}{f})
Strahlungsleistung (EIRP)
Die äquivalente isotrope Strahlungsleistung (engl. equivalent isotropically radiated power, EIRP) bezeichnet, in Bezug auf WLAN, eine Rechengröße der Abstrahlwirkung eines Gerätes inklusive Antennenzugewinn. Daraus folgt folgende Formel.
Sendeleistung des WLAN Moduls (dBm)
– Dämpfung der Kabel (komplette Länge, dB)
– Dämpfung der Stecker (dB)
– Dämpfung Sonstiger Adapter z.B. Blitzschutz (dB)
+ Antennengewinn (dBi)
Strahlungsleistung (EIRP)
Umrechnung dB / mW
Da im WLAN Umfeld fast alle Werte in Dezibel (dB) angegeben werden, sind Umrechnungen von Watt in Dezibel unumgänglich. Ferner werden hier eher die Werte in Milliwatt und Dezibel mit der Bezugsgröße 1mW (dBm) angegeben.
Formeln
L_p(dBm) = 10 \cdot log_{10}(\frac{P}{P_0}) dBm
P(mW) = 10^\frac{L_p}{10} \cdot 1mW
Die 3er und 10er Regel
Da man nicht immer einen Taschenrechner zur Hand hat und nicht immer alles im Kopf rechnen kann, kann man hier die 3er und 10er Regel anwenden.
- -3 dB = Halbierung der Leistung
- +3 dB = Verdopplung der Leistung
- -10dB = \frac{1}{10} der Leistung
- +10dB = 10x die Leistung
Beispiel
- 30 dBm = 1000 mW
- 23 dBm = 200 mW
- 20 dBm = 100 mW
- 17 dBm = 50 mW
- 14 dBm = 25 mW
Freiraumdämpfung
Die Reduzierung der Leistungsdichte bei der Ausbreitung der elektromagnetischen Wellen ohne Störeinflüsse im freien Raum beschreibt man als Freiraumdämpfung. Die Freiraumdämpfung ist ein wichtiges Kriterium zur Berechnung notwendiger Sendeleistungen für Richtfunkanwendungen.
Formeln
L = 10 \cdot log_{10}(\frac{4 \cdot \pi \cdot D(m)}{\lambda})^2
L = 10 \cdot log_{10}(\frac{4 \cdot \pi \cdot D(m) \cdot f}{c})^2
Fresnel Zone
Die Fesnel Zone beschreibt eine konzentrisch, ellipsenähnliche Hülle zwischen 2 Antennen bei hohen Distanzen (Richtfunk). Es gibt theoretisch unendliche Anzahl von Fresnel Zonen, aber wir betrachten hier nur die erste Zone Diese Hülle muss zu mindestens 60% frei von Behinderungen (z.B. Häuser, Bäume,..) sein, da sonst die Richtfunkstrecke nicht mehr funktioniert. Der Radius dieser Zone kann wie folgt berechnet werden.
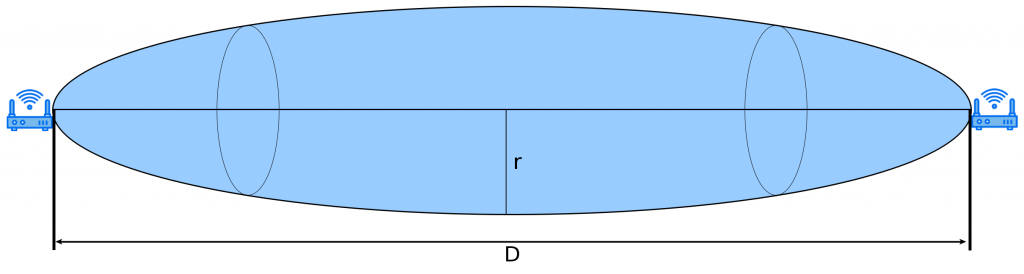
Formeln
Radius in Metern
r(m) = \frac{1}{2} \cdot \sqrt{\lambda \cdot D(km)}
r(m) = 8,657 \cdot \sqrt\frac{D(km)}{f}
Raidus in Feet
r(feet) = 36,03 \cdot \sqrt\frac{D(miles)}{f}
Erdkrümmung
Bei Richtfunk spielt die Erdkrümmung auch eine wichtige Rolle. Umso weiter der Transmitter vom Empfänger entfernt ist, umso höher ist die Höhenanpassung, die getätigt werden muss um eine Line of Sight (LoS) Verbindung zu erhalten. Die folgenden Formeln zeigen wie man den Höhenunterschied bzw. die notwendige Höhenanpassung berechnet.
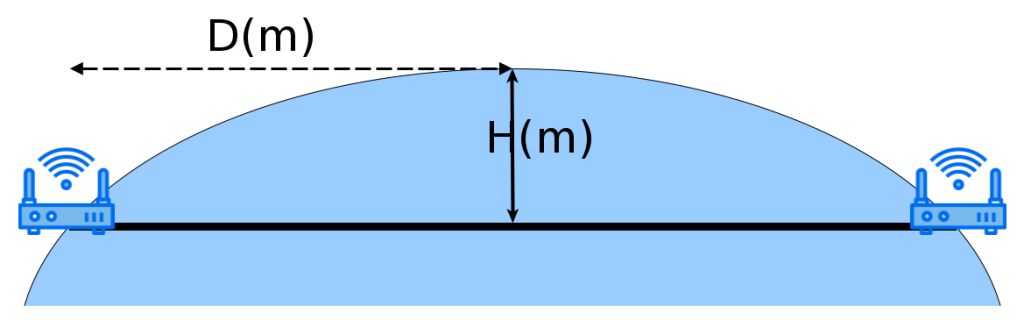
Formeln
r_{erde} = 6.371.000m
H(m) = \frac{D(m)^2}{(2 \cdot r_{erde})}
Kommentare von Waldo Rama